
Zang and Wunsch (2001, hereafter ZW2001) attempted a partial synthesis of variability that was, because of the available data, largely confined to the first phenomenon and in the Northern Hemisphere. However, because the statistics of trend determination in quantities such as sea level and volume transports depend directly upon the spectral limit of the frequency approaching zero, the appropriate significance calculations remain beyond reach, because low-frequency variability is indistinguishable from trends already present in the data.Īttention to oceanic variability has tended to focus on two particular, if disparate, phenomena: 1) the intense mesoscale eddy field with nominal time scales of months and spatial scales (here defined as wavelengths) of hundreds of kilometers 1 and 2) long period trends of decadal and longer time durations and (usually) of basin to global scale. The spectrum can be used to calculate statistical expectations of spatial average sea level and transport variations. The estimated spectrum also contains significant energy at all frequencies and wavenumbers in this range, including eastward-propagating motions, which are likely some combination of nonlinear spectral cascades, wave propagation, and wind-forced motions. The spectrum is dominated by motions along a “nondispersive” line, which is a robust feature of the data but for whose prominence a complete theoretical explanation is not available. These data are used to construct a purely empirical and analytical frequency–zonal wavenumber spectrum of ocean variability for periods between about 20 days and 15 yr and on spatial scales of about 200–10 000 km.
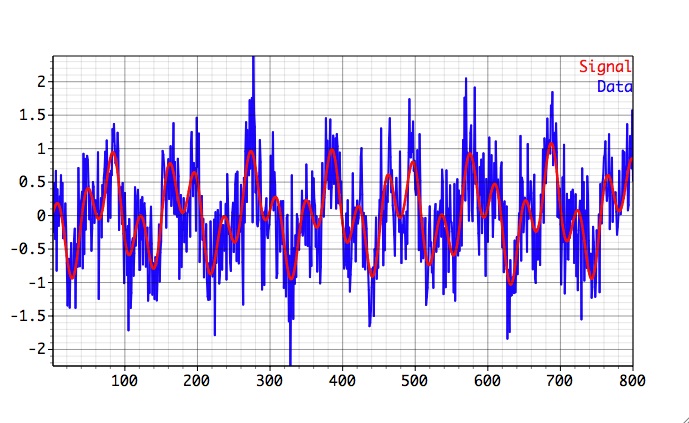
The time- and space-scale descriptive power of two-dimensional Fourier analysis is exploited to reanalyze the behavior of midlatitude variability as seen in altimetric data.


 0 kommentar(er)
0 kommentar(er)
